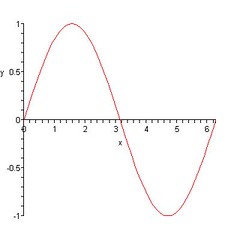
This is a normal sine curve, y=sin(x). But unlike what a lot of people think, the inverse DOES NOT exist for this particular domain.
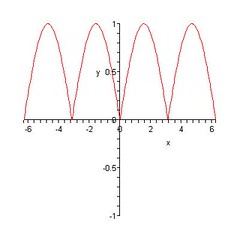
This is the modulus of a sine curve, y=modulus(sin(x)). This curve has worse properties than a normal sine curve. At least a sine curve is diffentiable everywhere. This one is not differentiable when y=0.
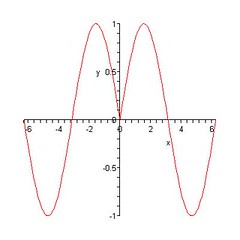
This is, y=sin(modulus(x)). Slightly better than the one above, but still has a point of non-differntiability. But, it's still bounded by 1 and -1. And that's the problem with the 2 basic trigonometric ratios, they are bounded.
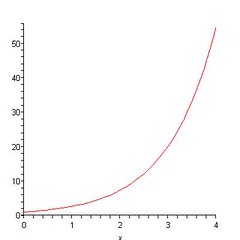
This is an exponential curve! This one is unbounded above, so it will continue to increase and at a very fast rate. Not just that the rate of increase is very special, because when you differntiate the function, you get back itself. That is very special! Show that you are steadily increasing rather than jumping up and down.